EL ARTE DE LAS MATEMÁTICAS.: LAS MATEMATICAS Y EL ARTE.

Las matemáticas y el arte están relacionados de varias maneras. De hecho, es frecuente encontrar las matemáticas descritas como un arte debido a la belleza o la elegancia de muchas de sus formulaciones, y se puede encontrar fácilmente su presencia en manifestaciones como la música, la danza, la pintura, la arquitectura, la escultura y las artes textiles.

Este artículo se centra en la influencia de las matemáticas en las artes visuales.

Nació el sábado
15de abril de 1452

Las matemáticas y el arte tienen una larga relación histórica. Está documentada la existencia de artistas matemáticos desde el siglo IV a. C., cuando el escultor griego Policleto escribió su "Canon", prescribiendo proporciones basadas en la relación 1:√2 para el desnudo masculino ideal. Curiosamente, cada vez son más frecuentes presuntas evidencias del uso del número áureo en el arte y la arquitectura antiguos, sin bases fiables que respalden estas teorías.

En el Renacimiento italiano, Luca Pacioli escribió el influyente tratado De divina proportione (1509), ilustrado con grabados en madera realizados por Leonardo da Vinci, sobre el uso de la proporción áurea en el arte.

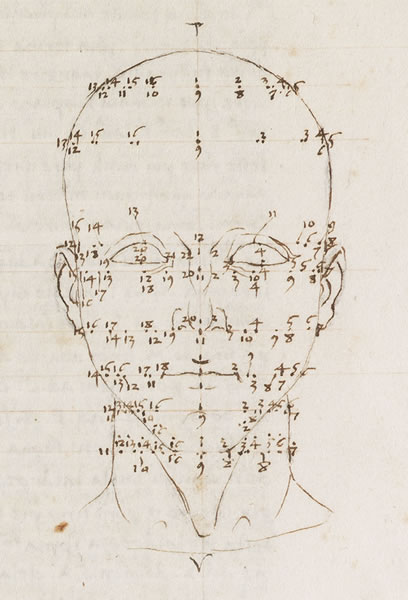Prospectiva
Pingendi
Piero della Francesca, desarrolló las ideas de Euclides sobre la perspectiva en tratados como De Prospectiva Pingendi y en sus propias pinturas. El grabador Alberto Durero efectuó numerosas referencias a las matemáticas en su obra, con trabajos como Melancolía I. En los tiempos modernos, el artista gráfico M. C. Escher hizo un uso intensivo del teselado y de la geometría hiperbólica con la ayuda del matemático Harold Scott MacDonald Coxeter, mientras que el movimiento De Stijl liderado por Theo van Doesburg y Piet Mondrian abarcó explícitamente las formas geométricas. Las matemáticas han inspirado las artes textiles tales como el quilting, el punto, el punto de cruz, el ganchillo, el bordado, la tejeduría, las alfombras y otras creaciones como el kilim. En el arte islámico, las simetrías son evidentes en formas tan variadas como el girih persa y el azulejo zellige marroquí, las pantallas mogolas jali de piedra perforada y las bóvedas decoradas con mocárabe.

El influjo directo de las matemáticas sobre el arte se evidencia en el uso de herramientas conceptuales como la perspectiva, el análisis de la simetría y en la presencia en diversas obras de objetos matemáticos que han ejercido una especial atracción sobre artistas de distintas épocas, como los poliedros o la banda de Möbius.

Magnus Wenninger creó poliedros estelados coloridos, originalmente como modelos para la enseñanza. Conceptos matemáticos como recursión y paradojas lógicas se pueden ver en las pinturas de René Magritte y en grabados de M. C. Escher.

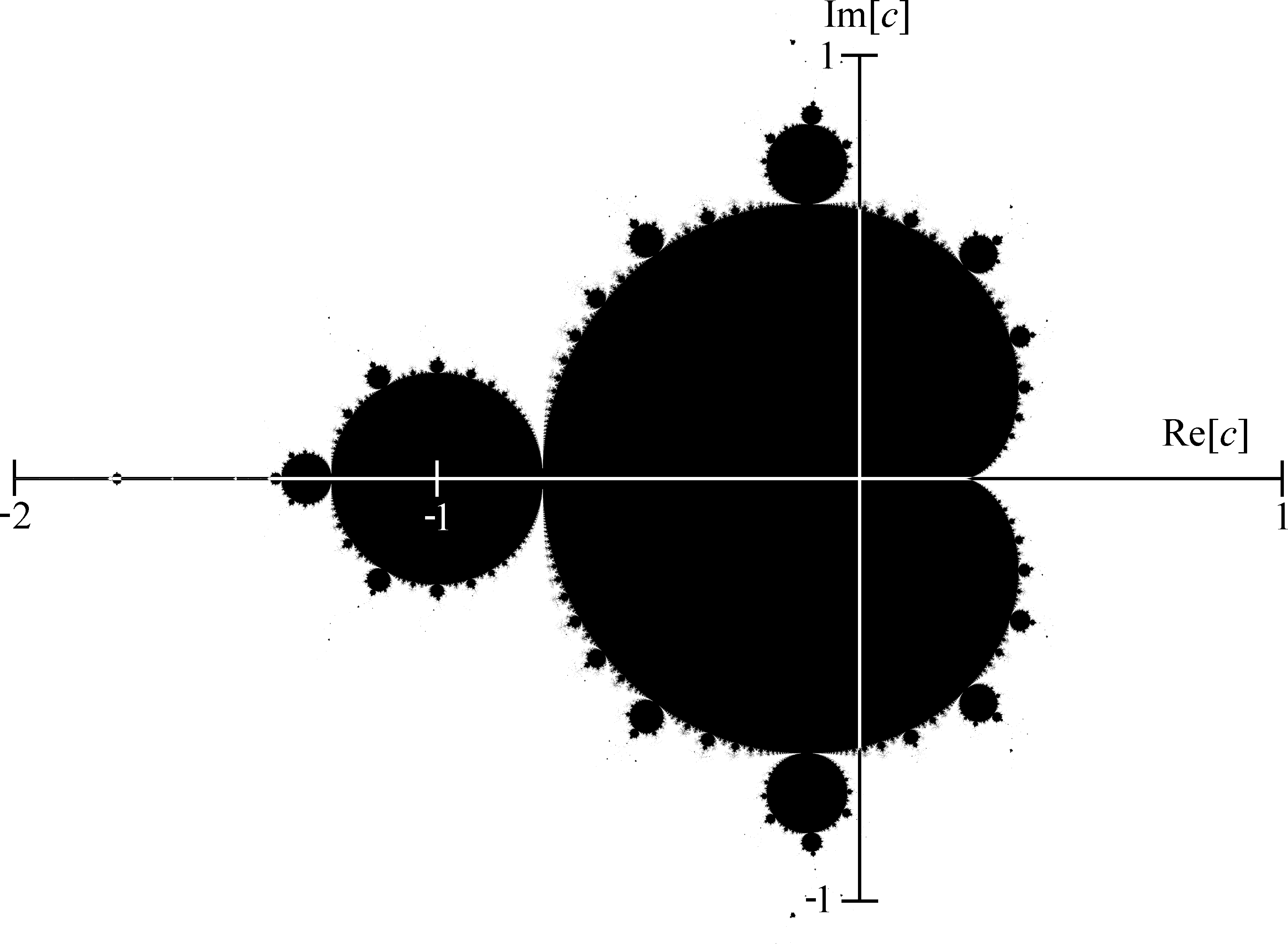
El arte computacional a menudo hace uso de fractales, incluido el conjunto de Mandelbrot, y, a veces, explora otros objetos matemáticos como los autómatas celulares. De forma controvertida, ligando la óptica con la pintura, el artista David Hockney ha argumentado que desde el Renacimiento en adelante la mayoría de los artistas utilizaron la cámara lúcida para dibujar representaciones precisas de escenas.

Otras relaciones incluyen el análisis algorítmico de las obras de arte mediante la fluorescencia de rayos X, o el hallazgo de que los batik tradicionales de diferentes regiones de la isla de Java tienen composiciones fractales.

El arte ha servido en ocasiones como estímulo para la investigación matemática, especialmente en el caso de la teoría de la perspectiva de Filippo Brunelleschi, que finalmente llevó a Girard Desargues al desarrollo de la geometría proyectiva. Una visión persistente, basada en última instancia en la noción pitagórica de armonía en la música, sostiene que el universo está organizado según relaciones numéricas, que Dios es el geómetra del mundo y que, por lo tanto, la geometría es sagrada, tal como queda reflejado en obras de arte como El anciano de los días de William Blake.

LAS MATEMATICAS COMO ARTE.

El matemático Jerry P. King describe las matemáticas como un arte, afirmando que "las claves de las matemáticas son la belleza y la elegancia y no el aburrimiento y los tecnicismos", y que la belleza es la fuerza motivadora de la investigación matemática. King cita el ensayo matemático publicado por Godfrey Harold Hardy en 1940, titulado Apología de un matemático. En este escrito, Hardy analiza por qué encuentra dos teoremas de la antigüedad clásica como de primera clase, a saber, la prueba de Euclides de que hay infinitos números primos, y la prueba de que la raíz cuadrada de 2 es un número irracional. King evalúa estos teoremas según los criterios de Hardy para estimar la elegancia matemática: "sobriedad, profundidad, generalidad, imprevisibilidad, inevitabilidad" y "economía" (las cursivas son de King), y describe la prueba como "estéticamente agradable".El matemático húngaro Paul Erdős estuvo de acuerdo en que las matemáticas poseían belleza, pero consideró las razones más allá de la explicación:

"¿Por qué son hermosos los números? Es como preguntar por qué es hermosa la Novena Sinfonía de Beethoven. Si no ves el porqué, nadie te lo puede explicar. Yo sé que los números son hermosos".

Herramientas matemáticas para el arte.

Octopod, obra de Mikael Hvidtfeldt Christensen. Arte algorítmico producido con el programa Structure Synth

Véanse también: Anexo:Lista de artistas matemáticos, Fractalismo y Arte computacional.

Las matemáticas aparecen en el sustrato de prácticamente todas las artes, como la música, la danza, la pintura, la arquitectura y la escultura. Cada una está asociado con las matemáticas de una manera particular. Gracias a su conexión con las artes visuales, las matemáticas pueden proporcionar herramientas para los artistas, como las reglas de la perspectiva descritas por Brook Taylor y Johann Heinrich Lambert, o los métodos de geometría descriptiva, posteriormente aplicados al modelado de sólidos por ordenador, y cuyos orígenes teóricos se remontan a Durero y a Gaspard Monge.

Los artistas de la Edad Media y del Renacimiento han utilizado y desarrollado ideas matemáticas mientras investigaban nuevas formas de llevar a cabo su trabajo artístico.

El uso de la perspectiva comenzó, a pesar de algunos intentos incipientes en la arquitectura de la antigua Grecia, con los pintores italianos.

Reglas como la del punto de fuga fueron formuladas por primera vez por Filippo Brunelleschi alrededor de 1413, y sus teorías influyeron definitivamente en Leonardo y en Durero.

El trabajo de Isaac Newton sobre el espectro óptico influyó en la teoría de los colores de un literato como Goethe y, a su vez, en artistas como philipp Otto Runge, J. M. W. Turner, los miembros de la Hermandad Prerrafaelita y sobre Vasili Kandinski.

Los artistas también pueden analizar la simetría de una escena, y trabajar sobre este concepto. Las mismas herramientas pueden ser aplicadas por matemáticos que están explorando el arte, o por artistas inspirados en las matemáticas, como M.C. Escher (inspirado en Harold Scott MacDonald Coxeter) o el arquitecto Frank Gehry, quien argumentó que el diseño asistido por computadora le permitió expresarse de una manera completamente nueva.

El artista Richard Wright argumenta que los objetos matemáticos que pueden construirse pueden verse "como procesos para simular fenómenos" o como obras de "arte computacional". Considera la naturaleza del pensamiento matemático, observando que los matemáticos conocían los fractales desde un siglo antes de que fueran reconocidos como tales.

Wright concluye afirmando que es apropiado someter los objetos matemáticos a cualquier método utilizado para "llegar a un acuerdo con conceptos culturales como el arte, la tensión entre objetividad y subjetividad, sus significados metafóricos y el carácter de los sistemas de representación". Da como ejemplos una imagen del conjunto de Mandelbrot, una imagen generada por un algoritmo de autómata celular y una imagen renderizada, y discute, con referencia al Test de Turing, si los productos de un algoritmo pueden ser arte.

Sasho Kalajdzievski, en su obra "Math and Art: An Introduction to Visual Mathematics (Matemáticas y Arte: una introducción a las matemáticas visuales) adopta un enfoque similar, analizando temas matemáticos visuales adecuados, como teselados, fractales y geometría hiperbólica.

Algunas de las primeras obras de arte computacional fueron creadas por "Drawing Machine 1", un sistema ideado por Desmond Paul Henry, que consistía en una computadora analógica basada en un visor de bombardero, exhibida en 1962.

La máquina era capaz de crear dibujos lineales complejos, abstractos, asimétricos o curvilíneos, pero repetitivos. Más recientemente, Hamid Naderi Yeganeh ha creado formas sugerentes de objetos del mundo real, como peces y aves, utilizando fórmulas que son sucesivamente variadas para dibujar familias de curvas o líneas en ángulo.

Artistas como Mikael Hvidtfeldt Christensen crean obras de arte algorítmico escribiendo rutinas para un sistema de software como Structure Synth: el artista dirige efectivamente el sistema para aplicar una combinación deseada de operaciones matemáticas a un conjunto de datos previajente elegido.

El matemático y físico teórico Henri Poincaré veía la geometría euclidiana como una de las muchas configuraciones posibles del espacio, en lugar de como una verdad objetiva absoluta. Picasso, en su obra de 1907 Las señoritas de Avignon utilizó la proyección en una cuarta dimensión para mostrar simultáneamente las figuras de frente y de perfil.

La posible existencia de una cuarta dimensión inspiró a los artistas la posibilidad de cuestionar la perspectiva clásica heredada del Renacimiento: la geometría no euclidiana se convirtió en una alternativa válida más.

El concepto de que la pintura podría expresarse matemáticamente, en color y forma, contribuyó al cubismo, el movimiento artístico que condujo al arte abstracto.

Metzinger, en 1910, escribió que "[Picasso] presenta una perspectiva móvil y gratuita, desde la que ese ingenioso matemático, Maurice Princet, ha deducido toda una geometría".

Era un artista que conceptualizaba las matemáticas, e invocaba un continuo n-dimensional con pretensiones estéticas. Le encantaba ver cómo los artistas se interedaban en las nuevas visiones espaciales desarrolladas por Schlegel y otros matemáticos. Tuvo éxito en este cometido.

El impulso de hacer modelos de enseñanza o investigación de formas matemáticas crea naturalmente objetos que tienen simetrías y formas sorprendentes o agradables.

superficies de Enneper
Este fundamento matemático era importante para él, ya que le permitía negar que el objeto era "abstracto", permitiéndole afirmar que era tan real como el orinal que Duchamp convirtió en una obra de arte. Admitió que la fórmula de la superficie de Enneper que definía el objeto "no significaba nada para mí, pero las formas en sí mismas eran tan variadas y auténticas como cualquier otra en la naturaleza".

Utilizó sus fotografías de los modelos matemáticos como figuras de su serie sobre las obras de William Shakespeare, como su pintura "Antony and Cleopatra" de 1934.

Los artistas Theo van Doesburg y Piet Mondrian fundaron el movimiento De Stijl, que pretendía "establecer un vocabulario visual de formas geométricas elementales comprensibles por todos y adaptables a cualquier disciplina".

Muchas de sus obras de arte consisten visiblemente en cuadrados y triángulos, a veces también con círculos. Los artistas de De Stijl trabajaron en pintura, mobiliario, diseño de interiores y arquitectura.

Las matemáticas del teselado, los poliedros, la configuración del espacio y la autorreferencia proporcionaron al artista gráfico M.C. Escher material de por vida para sus grabados en madera.

En el Boceto de la Alhambra, Escher demostró que es posible crear arte con polígonos o formas regulares como triángulos, cuadrados y hexágonos. También usó polígonos irregulares para teselar el plano y a menudo utilizó reflexiones y traslaciones para obtener patrones adicionales. Muchas de sus obras contienen construcciones imposibles, hechas con objetos geométricos que configuran una contradicción entre la proyección en perspectiva y las tres dimensiones, pero son agradables a la vista humana.

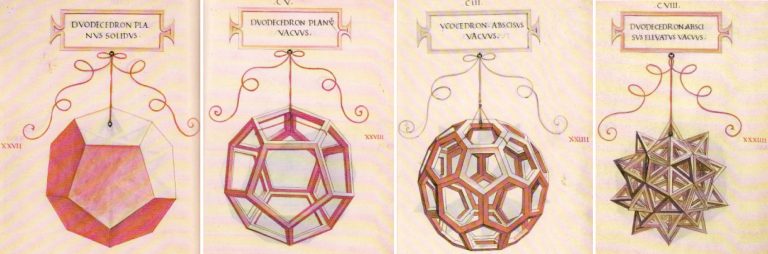
Algunos de los muchos dibujos de teselado de Escher se inspiraron en conversaciones con el matemático Harold Scott MacDonald Coxeter sobre la geometría hiperbólica.

Escher estaba especialmente interesado en cinco poliedros específicos, que aparecen muchas veces en su trabajo. Los sólidos platónicos (tetraedros, cubos, octaedros, dodecaedros e icosaedros) aparecen especialmente destacados en "Orden y Caos" y "Cuatro Sólidos Regulares"

Estas figuras a menudo se sitúan dentro de otras formas que distorsionan aún más el ángulo de visión y la conformación de los poliedros, proporcionando una obra de arte en perspectiva multifacética. La complejidad visual de las estructuras matemáticas, como las teselaciones y los poliedros, ha inspirado una gran variedad de obras de arte matemáticas.

Stewart Coffin diseñó rompecabezas poliédricos en maderas raras y hermosas.

George W. Hart trabajó en la teoría de poliedros y esculpió objetos inspirados en ellos

Magnus Wenninger realizó modelos de poliedros estelados complejos.

Las perspectivas distorsionadas con efectos de anamorfosis se han explorado en el arte desde el siglo XVI, cuando Hans Holbein el Joven incorporó un cráneo severamente distorsionado en su pintura "Los embajadores" de 1533.

Las matemáticas propias de la topología han inspirado a varios artistas en los tiempos modernos. El escultor John Robinson (1935-2007) creó obras como Gordian Knot y Bands of Friendship, mostrando la teoría de nudos en bronce pulido.